ZuoTiJia
0%

Pytorch入门

发表于 更新于

本文记录pytorch的入门使用，并且训练一个简单的线性回归模型。

安装

国内的话

1
pip install torch torchvision torchaudio -i https://pypi.tuna.tsinghua.edu.cn/simple/

之后运行如下代码测试

1
2
import torch
print(torch.__version__)

我的运行结果：

1.7.1

这就说明安装成功了

实现一个简单的线性回归训练

我这里示例用的是波士顿房价预测

数据集在此下载：

链接: https://pan.baidu.com/s/1BbUaubMigMAS_FKiaBIrdA 提取码: iij2

在这个数据集里

影响波士顿的房价的因素有13个

我们画表格来展现关系

x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 y
… … … … … … … … … … … … … …

有点像关系型数据库

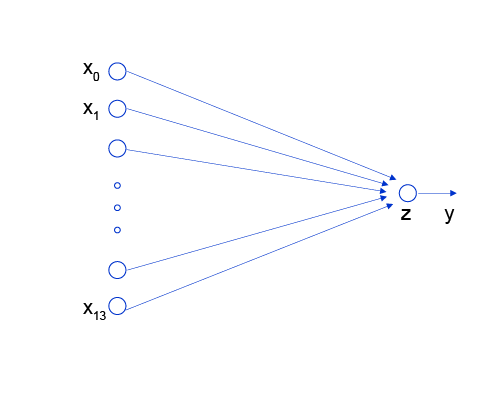
很显然神经网络是如下

我们的目标是通过训练，找到y = wx+b这个方程中最适合的w和b

首先把需要的库import

1
2
3
4
import torch
import torch.nn as nn           #神经网络工具箱
import torch.utils.data as Data #加载数据用的
import numpy as np

1.规定训练参数

第一步一般是规定训练中的各种参数

1
2
3
4
5
6
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu') #规定训练设备
input_size = 13 #这是输入网络的因素数量
output_size = 1 #输出的结果的数量
num_epochs = 2000 #训练的轮数
learning_rate = 0.01 #学习率
batch_size = 100 #把数据乱序拆分训练，每一份是100

这里显然我们输入是13个变量输出一个变量

这里采用的是随机梯度下降法，因此要把数据集乱序拆分成一个个batch,每轮训练完这些batch再开始下一轮

训练设备中 ‘cuda:0’中的0指的是第一块显卡，简单的模型只需一张卡就好了

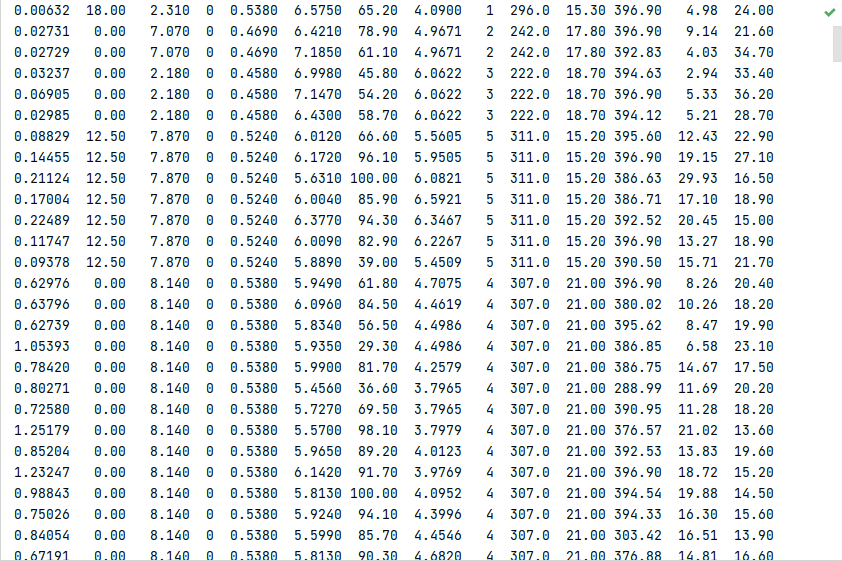
2.加载数据集

数据文本格式如下

我们使用numpy来读这个文本

1
2
data = np.fromfile('housing.data', dtype=float, sep=' ')
data = data.reshape(-1, 14)

numpy读出的是个一维的向量，我们要把它的形状变成一行14个

为什么要用32位浮点数，double不行吗？

市面上的显卡大部分都是游戏显卡，大部分都只支持32位浮点数运算

由于没有专门的测试集，所以我们要手动划分，这里我们按80%训练集20%测试集

我们还发现这13个因素的数据范围不固定，一般要先归一化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#归一化加划分数据
def Nomalize(data, ratio=0.8): #ratio是训练集占比
    offset = int(data.shape[0]*ratio) #计算训练集样本数量
    # 归一化操作
    train_data = data[:offset] 
    max, min = train_data.max(axis=0), train_data.min(axis=0)
    for i in range(data.shape[1]-1):
        data[:, i] = (data[:, i]-min[i])/(max[i]-min[i])
    #
    data = torch.from_numpy(data)#从numpy array转到torch的tensor 
    #划分训练集和测试集
    train_data = data[:offset]
    test_data = data[offset:]
    return train_data, test_data

这里我们用函数封装了起来

pytorch给我们一个加载数据集的抽象类

torch.utils.data.Dataset

我们通过这个类来加载我们的训练集， 我们必须复写类中如下三个方法

1
2
3
4
5
6
7
8
9
class HouseDataset(torch.utils.data.Dataset):
    def __init__(self, data):
        self.data = data.float()
    def __getitem__(self, item): #提供索引访问方法 类似 set[0]
        x = self.data[item][:-1]
        y = self.data[item][-1:]
        return x, y              #返回的是输入因素和输出结果
    def __len__(self):
        return len(self.data)    #返回的是数据集的长度

之后实例化类

1
2
3
4
5
6
7
8
train_data, test_data = Nomalize(data) #调用写的归一化函数
train_dataset = HouseDataset(train_data) 
test_dataset = HouseDataset(test_data)

#batch_size就是我们之前定义的每一小份的份数,shuffle是打乱顺序的意思
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
                                           batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=len(test_dataset))

3.构建网络

我们只需继承 nn.Moudule 并且重写init和forward方法即可

1
2
3
4
5
6
7
class Net(nn.Module):
    def __init__(self, inputsize):
        super(Net, self).__init__()             #这行必须写，就当是套路就行了
        self.linear = nn.Linear(input_size, output_size)    #这个网络里只有一个线性层
    def forward(self, x):                       #向前传播
        return self.linear(x)

nn里面还有卷积层， 池化层，归一层等等，这里我们只用线性层就行

4.实例化网络和优化器，定义损失函数

1
2
3
4
net = Net(input_size).to(device) #把模型丢到预定义的设备中
criterion = nn.MSELoss()
# 这里第一个参数是模型中要优化的参数，pytorch会自动构建
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)

这里用的损失函数是MSELoss

优化器是SGD

5.开始训练

这里就是套路了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
total_step = len(train_loader)#每一轮训练的份数
for epoch in range(num_epochs):
    for i, (x, y) in enumerate(train_loader):
        x = x.to(device)
        y = y.to(device)

        out = net(x)
        loss = criterion(out, y)
        
        optimizer.zero_grad() #这个是将计算图中所有梯度清零
        loss.backward()       #从后往前计算梯度
        optimizer.step()      #优化器优化    
        
        print ('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}' 
                   .format(epoch+1, num_epochs, i+1, total_step, loss.item()))

6.画图看看拟合状况

1
2
3
4
5
6
7
8
9
10
11
12
import matplotlib.pyplot as plt
with torch.no_grad(): #因为我们要测试就不需要计算梯度了
    for i, (x, y) in enumerate(test_loader):
        x = x.to(device)
        out = net(x)
        out = out.detach().numpy()
        y = y.detach().numpy()
        out.shape = (-1, 1)
        y.shape = (-1, 1)
        plt.plot(out, label='拟合')
        plt.plot(y, label='原始数据')
        plt.show()

代码汇总

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import torch
import torch.nn as nn 			#神经网络工具箱
import torch.utils.data as Data #加载数据用的
import numpy as np

device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu') #规定训练设备
input_size = 13	#这是输入网络的因素数量
output_size = 1 #输出的结果的数量
num_epochs = 200 #训练的轮数
learning_rate = 0.01 #学习率
batch_size = 100 #把数据乱序拆分训练，每一份是100

data = np.fromfile('housing.data', dtype=float, sep=' ')
data = data.reshape(-1, 14)

def Nomalize(data, ratio=0.8): #ratio是训练集占比
    offset = int(data.shape[0]*ratio) #计算训练集样本数量
    # 归一化操作
    train_data = data[:offset]
    max, min = train_data.max(axis=0), train_data.min(axis=0)
    for i in range(data.shape[1]-1):
        data[:, i] = (data[:, i]-min[i])/(max[i]-min[i])
	#
    data = torch.from_numpy(data)#从numpy array转到torch的tensor
    #划分训练集和测试集
    train_data = data[:offset]
    test_data = data[offset:]
    return train_data, test_data

class HouseDataset(torch.utils.data.Dataset):
    def __init__(self, data):
        self.data = data.float()
    def __getitem__(self, item): #提供索引访问方法 类似 set[0]
        x = self.data[item][:-1]
        y = self.data[item][-1:]
        return x, y              #返回的是输入因素和输出因素
    def __len__(self):
        return len(self.data)    #返回的是数据集的长度

train_data, test_data = Nomalize(data) #调用写的归一化函数
train_dataset = HouseDataset(train_data)
test_dataset = HouseDataset(test_data)

#batch_size就是我们之前定义的每一小份的份数,shuffle是打乱顺序的意思
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
                                           batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_dataset, batch_size=len(test_dataset))

print(train_dataset)
class Net(nn.Module):
    def __init__(self, inputsize):
        super(Net, self).__init__() 			#这行必须写，就当是套路就行了
        self.linear = nn.Linear(input_size, output_size) 	#这个网络里只有一个线性层
    def forward(self, x):						#向前传播
        return self.linear(x)

net = Net(input_size).to(device) #把模型丢到预定义的设备中
criterion = nn.MSELoss()
# 这里第一个参数是模型中要优化的参数，pytorch会自动构建
optimizer = torch.optim.SGD(net.parameters(), lr=learning_rate)

total_step = len(train_loader)  # 每一轮训练的份数
for epoch in range(num_epochs):
    for i, (x, y) in enumerate(train_loader):
        x = x.to(device)
        y = y.to(device)

        out = net(x)
        loss = criterion(out, y)

        optimizer.zero_grad()  # 这个是将计算图中所有梯度清零
        loss.backward()  # 从后往前计算梯度
        optimizer.step()  # 优化器优化

        # print('Epoch [{}/{}], Step [{}/{}], Loss: {:.4f}'
        #      .format(epoch + 1, num_epochs, i + 1, total_step, loss.item()))

import matplotlib.pyplot as plt
with torch.no_grad(): #因为我们要测试就不需要计算梯度了
    for i, (x, y) in enumerate(test_loader):
        x = x.to(device)
        out = net(x)
        y = y.numpy()
        out = out.cpu().detach().numpy()
        out.shape = (-1, 1)
        y.shape = (-1, 1)
        plt.plot(out, label='拟合')
        plt.plot(y, label='原始数据')
        plt.show()